quadrature_mod Module Reference

Data Types
type	quadrature_t

Functions/Subroutines
type(quadrature_t) function, public	gauss (npts)
real(kind=longdouble_kind) function, dimension(np1), private	gauss_pts (np1)
real(kind=longdouble_kind) function, dimension(np1), private	gauss_wts (np1, gpts)
subroutine, public	test_gauss (npts)
type(quadrature_t) function, public	gausslobatto (npts)
real(kind=longdouble_kind) function, dimension(np1), private	gausslobatto_pts (np1)
real(kind=longdouble_kind) function, dimension(np1), private	gausslobatto_wts (np1, glpts)
subroutine, public	test_gausslobatto (npts)
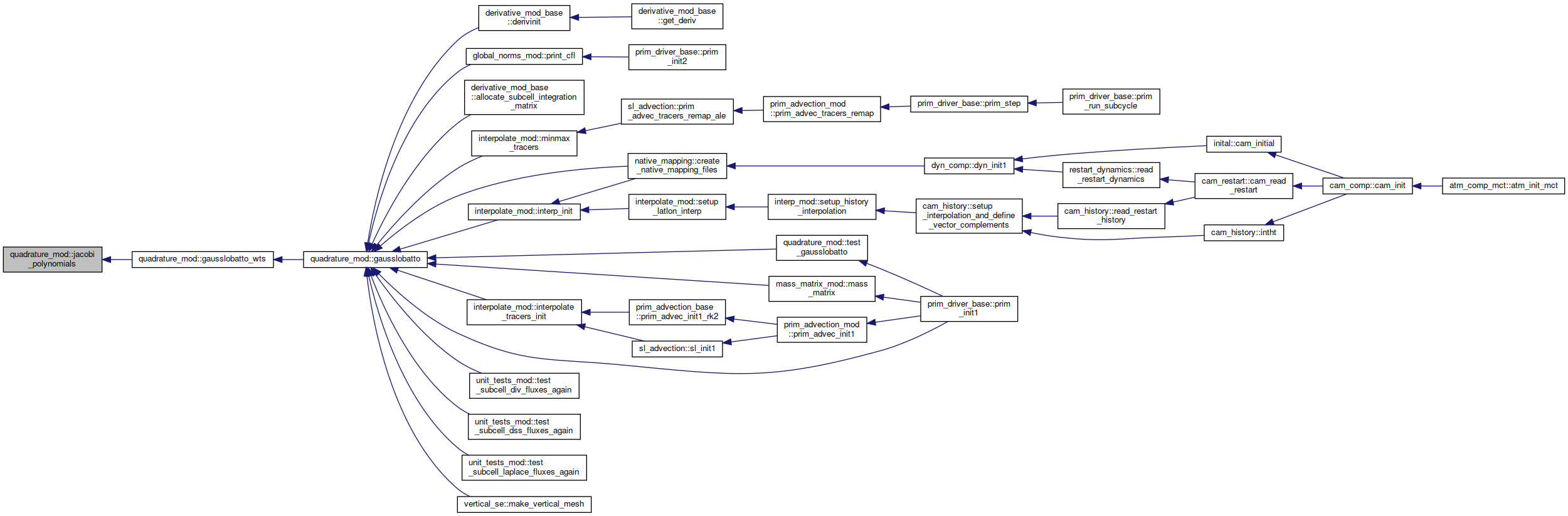
subroutine, public	jacobi (n, x, alpha, beta, jac, djac)
real(kind=longdouble_kind) function, dimension(npoints), private	jacobi_polynomials (n, alpha, beta, npoints, x)
real(kind=longdouble_kind) function, dimension(npoints), private	jacobi_derivatives (n, alpha, beta, npoints, x)
real(kind=longdouble_kind) function, dimension(n+1), public	legendre (x, N)
real(kind=longdouble_kind) function, dimension(n), public	quad_norm (gquad, N)
subroutine, private	trapn (f, a, b, N, it, s)
real(kind=real_kind) function, public	trapezoid (f, a, b, eps)
real(kind=real_kind) function, public	simpsons (f, a, b, eps)
real(kind=real_kind) function, public	gaussian_int (f, a, b, gs)

Function/Subroutine Documentation

gauss()

type (quadrature_t) function, public quadrature_mod::gauss

(

integer, intent(in)

npts

)

Here is the call graph for this function:

Here is the caller graph for this function:

gauss_pts()

real (kind=longdouble_kind) function, dimension(np1), private quadrature_mod::gauss_pts ( integer, intent(in)  np1 )

private

Here is the call graph for this function:

Here is the caller graph for this function:

gauss_wts()

real (kind=longdouble_kind) function, dimension(np1), private quadrature_mod::gauss_wts ( integer, intent(in)  np1, real (kind=longdouble_kind), dimension(np1), intent(in)  gpts  )

private

Here is the call graph for this function:

Here is the caller graph for this function:

gaussian_int()

real(kind=real_kind) function, public quadrature_mod::gaussian_int	(		f,
		real(kind=real_kind), intent(in)	a,
		real(kind=real_kind), intent(in)	b,
		type(quadrature_t), intent(in)	gs
	)

gausslobatto()

type (quadrature_t) function, public quadrature_mod::gausslobatto

(

integer, intent(in)

npts

)

Here is the call graph for this function:

Here is the caller graph for this function:

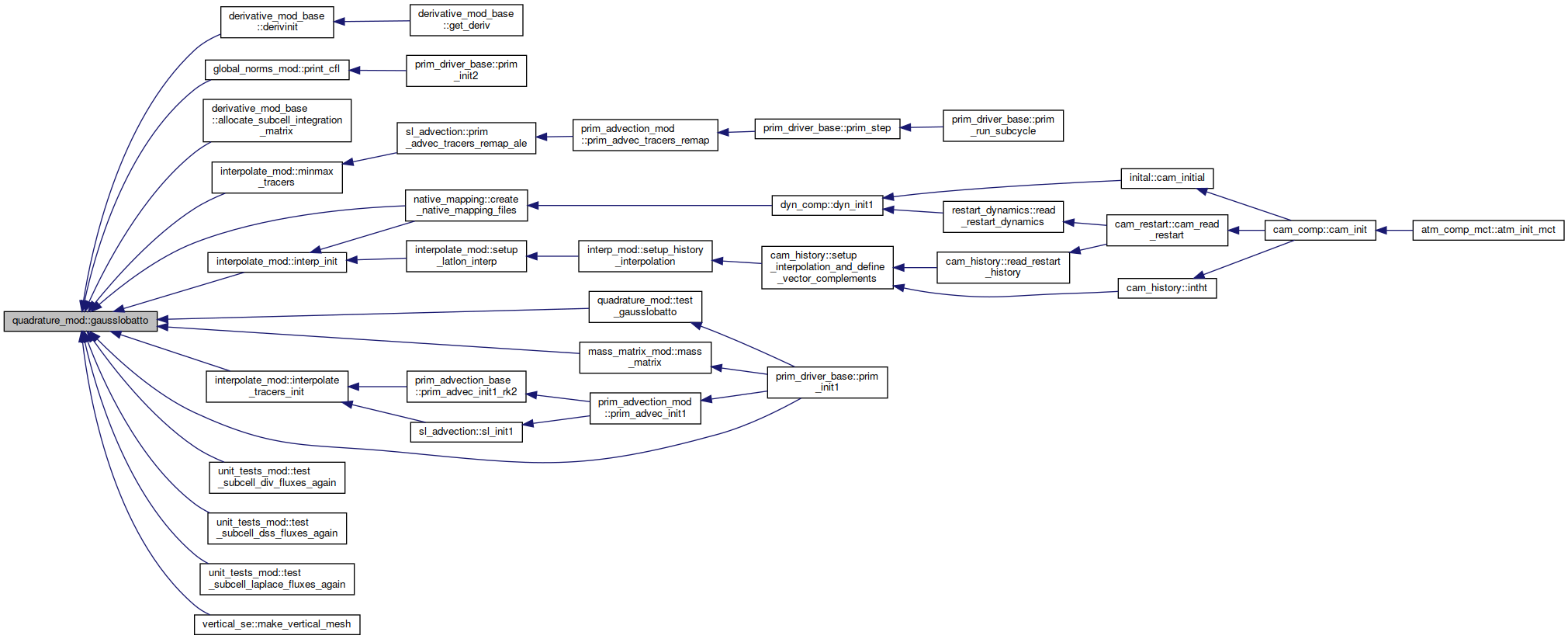
gausslobatto_pts()

real (kind=longdouble_kind) function, dimension(np1), private quadrature_mod::gausslobatto_pts ( integer, intent(in)  np1 )

private

Here is the call graph for this function:

Here is the caller graph for this function:

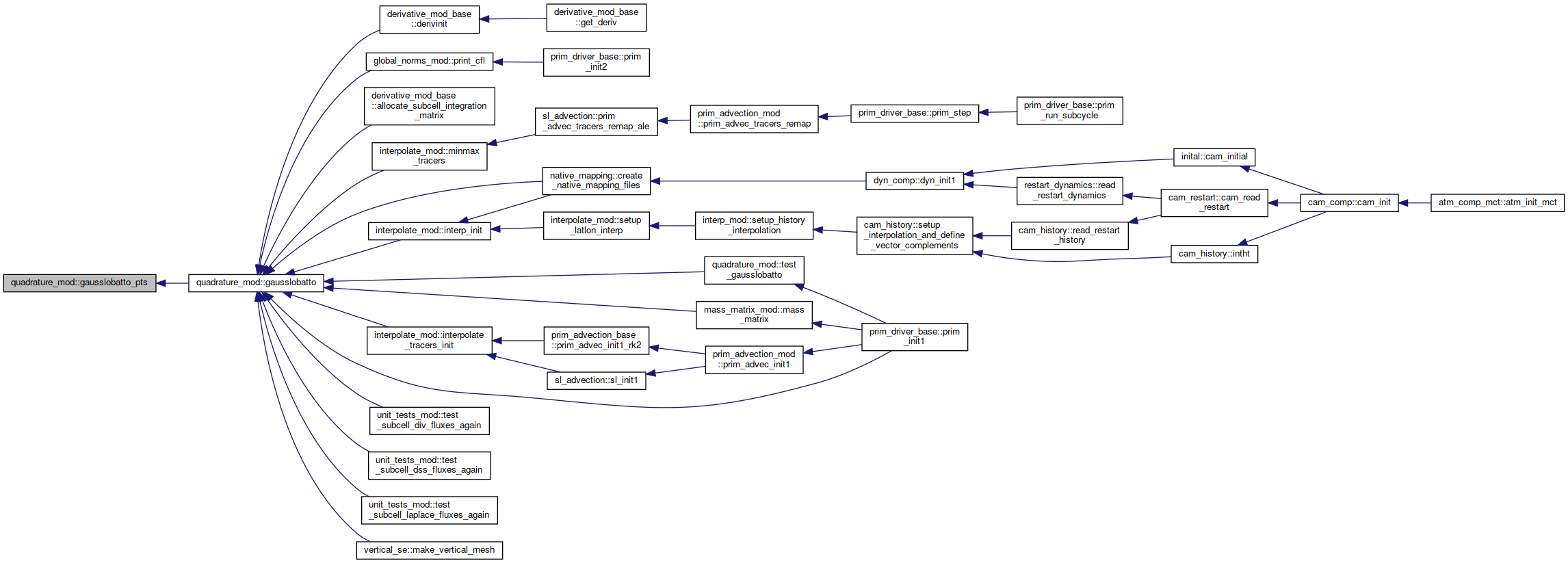
gausslobatto_wts()

real (kind=longdouble_kind) function, dimension(np1), private quadrature_mod::gausslobatto_wts ( integer, intent(in)  np1, real (kind=longdouble_kind), dimension(np1), intent(in)  glpts  )

private

Here is the call graph for this function:

Here is the caller graph for this function:

jacobi()

subroutine, public quadrature_mod::jacobi	(	integer, intent(in)	n,
		real (kind=longdouble_kind), intent(in)	x,
		real (kind=longdouble_kind), intent(in)	alpha,
		real (kind=longdouble_kind), intent(in)	beta,
		real (kind=longdouble_kind), dimension(0:n)	jac,
		real (kind=longdouble_kind), dimension(0:n)	djac
	)

Here is the caller graph for this function:

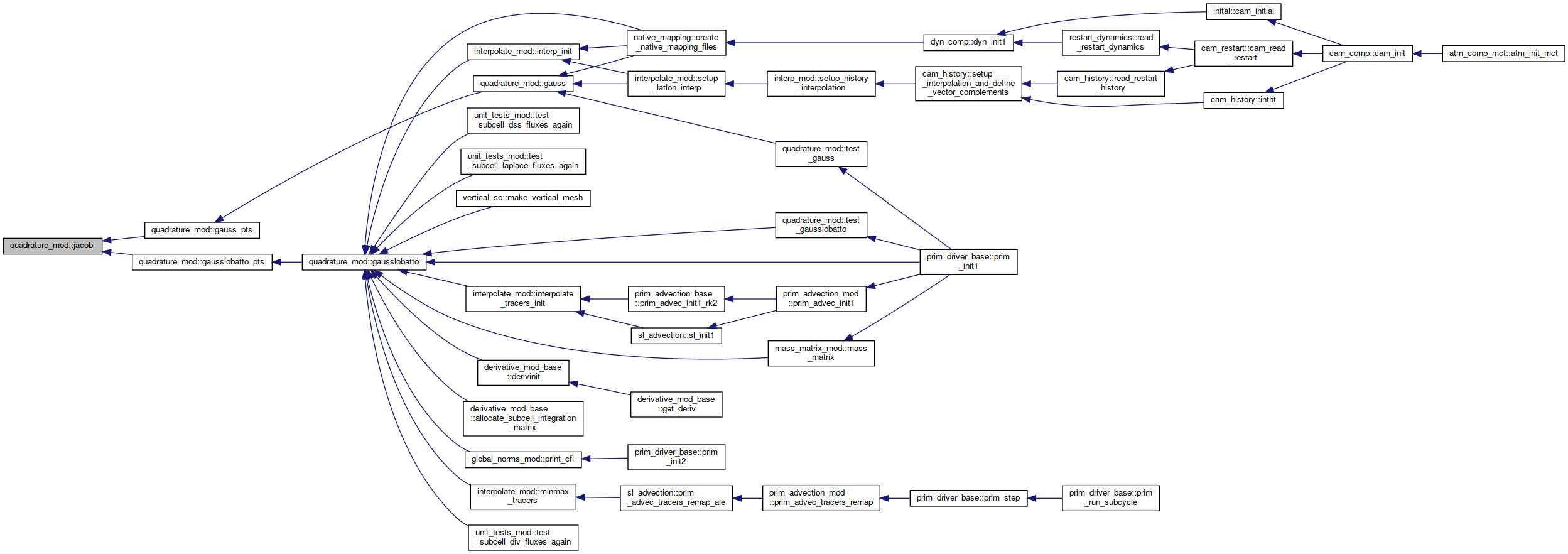
jacobi_derivatives()

real (kind=longdouble_kind) function, dimension(npoints), private quadrature_mod::jacobi_derivatives ( integer, intent(in)  n, real (kind=longdouble_kind), intent(in)  alpha, real (kind=longdouble_kind), intent(in)  beta, integer, intent(in)  npoints, real (kind=longdouble_kind), dimension(npoints), intent(in)  x  )

private

Here is the caller graph for this function:

jacobi_polynomials()

real (kind=longdouble_kind) function, dimension(npoints), private quadrature_mod::jacobi_polynomials ( integer, intent(in)  n, real (kind=longdouble_kind)  alpha, real (kind=longdouble_kind)  beta, integer, intent(in)  npoints, real (kind=longdouble_kind), dimension(npoints)  x  )

private

Here is the caller graph for this function:

legendre()

real (kind=longdouble_kind) function, dimension(n+1), public quadrature_mod::legendre	(	real (kind=longdouble_kind)	x,
		integer	N
	)

quad_norm()

real (kind=longdouble_kind) function, dimension(n), public quadrature_mod::quad_norm	(	type (quadrature_t), intent(in)	gquad,
		integer, intent(in)	N
	)

Here is the call graph for this function:

simpsons()

real(kind=real_kind) function, public quadrature_mod::simpsons	(		f,
		real(kind=real_kind), intent(in)	a,
		real(kind=real_kind), intent(in)	b,
		real(kind=real_kind), intent(in)	eps
	)

Here is the call graph for this function:

test_gauss()

subroutine, public quadrature_mod::test_gauss

(

integer, intent(in)

npts

)

Here is the call graph for this function:

Here is the caller graph for this function:

test_gausslobatto()

subroutine, public quadrature_mod::test_gausslobatto

(

integer, intent(in)

npts

)

Here is the call graph for this function:

Here is the caller graph for this function:

trapezoid()

real(kind=real_kind) function, public quadrature_mod::trapezoid	(		f,
		real(kind=real_kind), intent(in)	a,
		real(kind=real_kind), intent(in)	b,
		real(kind=real_kind), intent(in)	eps
	)

Here is the call graph for this function:

trapn()

subroutine, private quadrature_mod::trapn (   f, real(kind=real_kind), intent(in)  a, real(kind=real_kind), intent(in)  b, integer, intent(in)  N, integer, intent(inout)  it, real(kind=real_kind), intent(inout)  s  )

private

Here is the caller graph for this function: